Alles ist ungenau bis zu einem gewissen Grad, den man erst
bemerkt, wenn man versucht hat, etwas genau zu machen.
Bertrand Russel
The Philosophy of Logical Atomism
Die Theorie unscharfer Mengen, der Fuzzy-Mengen, kann sowohl als eine Verallgemeinerung der klassischen Mengenlehre als auch als eine Verallgemeinerung der zweiwertigen (dualen) Logik angesehen werden [Zimmermann 1993]. Da die verallgemeinerten Mengentheorie leichter nachzuvollziehen ist als die Theorie der verallgemeinerten Logik, wird hier die Fuzzy Logic über die Fuzzy-Mengen eingeführt.
Cantor hatte Mengen wie folgt definiert [Mayer 1993, Seite 10]: eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohlunterschiedenen Objekten unserer Anschauung oder unseres Denkens (welche Elemente von M genannt werden) zu einem Ganzen.
Die Theorie der Fuzzy-Mengen erweitert nun die Begriffe der klassischen Mengenlehre von Cantor mit den dort entwickelten Operationen (vgl. Abbildung 3). Die Wohlbestimmtheit und Wohlunterschiedenheit wird dabei aufgegeben.
In der bekannten Mengenlehre nach Cantor gehört ein Element entweder zu einer Menge,
oder es gehört nicht dazu. Es gibt keine Zwischenwerte, die es Elementen erlauben, nur
teilweise in einer Menge enthalten zu sein. Mathematisch kann also der Zugehörigkeitsgrad ![]() eines Elementes e zu einer Menge M aus einem Universum U wie folgt beschrieben werden:
eines Elementes e zu einer Menge M aus einem Universum U wie folgt beschrieben werden:
![]()
Diese charakteristische Funktion ``scharfer'' Mengen (crisp set) kann verallgemeinert werden, so daß jedem Element aus der Universalmenge U ein Wert aus einem gewissen Intervall (aus Einfachkeitsgründen üblicherweise [0,1]) zugewiesen wird, der den Mitgliedschaftsgrad von den Elementen in einer Menge definiert. So eine Funktion wird auch als Mitglieds- oder Zugehörigkeitsfunktion bezeichnet. Diese kann wir folgt zur Definition von Fuzzy-Mengen benutzt werden:
Eine Fuzzy-Menge (fuzzy set) ![]() ist
eine Abbildung von einem Universum U in das Einheitsintervall [0,1]:
ist
eine Abbildung von einem Universum U in das Einheitsintervall [0,1]:
![]()
Die Fuzzy-Menge ![]() ordnet jedem Element
ordnet jedem Element ![]() den Zugehörigkeitsgrad
den Zugehörigkeitsgrad ![]() aus dem Intervall [0,1] zu.
Dabei bedeutet
aus dem Intervall [0,1] zu.
Dabei bedeutet ![]() , daß
, daß ![]() nicht zu
nicht zu ![]() gehört,
gehört,
![]() , daß
, daß ![]() zur Hälfte zu
zur Hälfte zu ![]() gehört, und
gehört, und ![]() , daß
, daß ![]() ganz zu
ganz zu
![]() gehört. In der Praxis werden Mitgliedsfunktion und Fuzzy-Menge synonym benutzt.
gehört. In der Praxis werden Mitgliedsfunktion und Fuzzy-Menge synonym benutzt.
Es gibt mehrere Beschreibungsmöglichkeiten für Fuzzy-Mengen:
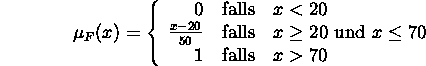
![]()
Diese natürlich nur bei endlicher Universalmenge sinnvolle Darstellungsart wird im Zusammenhang mit Fuzzy Logic oft wie folgt geschrieben:
![]()
Fuzzy-Mengen können semantisch auf zwei verschiedene Arten interpretiert werden:
Üblicherweise werden zur Beschreibung von Fuzzy-Mengen hauptsächlich
Trapezfunktionen (Abbildung 5),
da sie Ausdrücke wie ``ungefähr zwischen ![]() und
und ![]() recht gut wiedergeben,
Dreiecke (Abbildung 6) oder auch Glockenkurven,
da sie Ausdrücke wie ``etwa m'' nahekommen, oder
einzene Punkte für diskrete Fuzzy-Mengen (Abbildung 7).
Trapeze, Dreiecke und einzelne Punkte werden wegen ihrer Einfachheit und
mathematischen Eigenschaften besonders oft zur Beschreibung von Fuzzy-Mengen
verwendet.
recht gut wiedergeben,
Dreiecke (Abbildung 6) oder auch Glockenkurven,
da sie Ausdrücke wie ``etwa m'' nahekommen, oder
einzene Punkte für diskrete Fuzzy-Mengen (Abbildung 7).
Trapeze, Dreiecke und einzelne Punkte werden wegen ihrer Einfachheit und
mathematischen Eigenschaften besonders oft zur Beschreibung von Fuzzy-Mengen
verwendet.
Zwei entscheidende Kenngrößen für Fuzzy-Mengen sind ihre Einflußbreite (= Support, Träger)
und ihre Toleranz.
Die Einflußbreite einer Fuzzy-Menge ![]() in der Universalmenge U ist
die (scharfe) Menge aller Elemente von U, die einen positiven Mitgliedsgrad haben:
in der Universalmenge U ist
die (scharfe) Menge aller Elemente von U, die einen positiven Mitgliedsgrad haben:
![]()
Die Toleranz toll beschreibt, in welchem Intervall ![]() der Zugehörigkeitsgrad gleich 1 ist,
also
der Zugehörigkeitsgrad gleich 1 ist,
also
![]()
Der Einflußbereich von trapezförmigen Mengen ist nach Abbildung 5 also
das Intervall ![]() , die Toleranz
, die Toleranz ![]() .
.
Ist ![]() eine Fuzzy-Menge in U, so heißt
eine Fuzzy-Menge in U, so heißt
![]()
die Höhe von ![]() .
. ![]() heißt eine normale Fuzzy-Menge, wenn
heißt eine normale Fuzzy-Menge, wenn ![]() gilt, ansonsten subnormal (vgl. Abbildung 8).
gilt, ansonsten subnormal (vgl. Abbildung 8).
Für den praktischen Einsatz der Fuzzy-Logic ist es wichtig, daß nur mit normalen Fuzzy-Mengen gearbeitet wird, da diese mathematische Vorteile besitzen.
Eine Fuzzy-Menge ![]() in U heißt leer, wenn
in U heißt leer, wenn
![]()
Eine Fuzzy-Menge ![]() in U heißt universell, wenn
in U heißt universell, wenn
![]()
Eine Fuzzy-Menge ![]() heißt Fuzzy-Teilmenge einer Fuzzy-Menge
heißt Fuzzy-Teilmenge einer Fuzzy-Menge ![]() auf
der Universalmenge U, wenn gilt
auf
der Universalmenge U, wenn gilt
![]()
Schreibweise: ![]()
Eine Fuzzy-Menge kann nicht nur durch die oben beschriebenen vertikalen
Darstellungsarten beschrieben werden, sondern auch durch alle ihre ![]() -Schnitte,
die im folgenden definiert werden.
Es sei
-Schnitte,
die im folgenden definiert werden.
Es sei ![]() eine Fuzzy-Menge auf der Grundmenge U und
eine Fuzzy-Menge auf der Grundmenge U und ![]() . Dann
heißt
. Dann
heißt
![]()
der Schnitt der Fuzzy-Menge ![]() in der Höhe
in der Höhe ![]() (vgl. Abbildung 11).
(vgl. Abbildung 11).
![]() -Schnitte von Fuzzy-Mengen sind wieder klassische Mengen.
-Schnitte von Fuzzy-Mengen sind wieder klassische Mengen.
Diese Darstellungsart wird oft benutzt, wenn Fuzzy-Mengen in Computern modelliert werden sollen.
Man beschränkt sich dabei auf eine sinnvolle Anzahl von ![]() -Schnitten und
speichert diese in normaler Form, z.B. als Intervalle ab. Abbildung
12 verdeutlicht dies.
-Schnitten und
speichert diese in normaler Form, z.B. als Intervalle ab. Abbildung
12 verdeutlicht dies.
Eines der Hauptprobleme bei der Entwicklung von Fuzzy-Systemen ist die Wahl geeigneter Zugehörigkeitsfunktionen. Die Analyse von vielen Anwendungen hat gezeigt, daß es oft gar nicht auf exakte Werte in dem speziellen Intervall [0,1] ankommt, sondern nur auf Größenordnungen.
In manchen Fällen kann es daher sinnvoll sein, anstatt des Intervalls [0, 1] einen
beliebigen
Verband![]()
![]() zu betrachten, der eine
rein qualitative Anordnung der in L enthaltenen Zugehörigkeitsgrade
zum Ausdruck bringt. Falls es z.B. eine totale Ordnung auf L gibt
(z.B. unmöglich < unwahrscheinlich < kann sein <
wahrscheinlich < sicher),
also für alle
zu betrachten, der eine
rein qualitative Anordnung der in L enthaltenen Zugehörigkeitsgrade
zum Ausdruck bringt. Falls es z.B. eine totale Ordnung auf L gibt
(z.B. unmöglich < unwahrscheinlich < kann sein <
wahrscheinlich < sicher),
also für alle ![]() gilt
gilt ![]() oder l > l', so ist
oder l > l', so ist
![]() durch
durch
![]()
definiert.
Diese Überlegung führt zu dem gegenüber Fuzzy-Mengen verallgemeinerten
Begriff der L-Fuzzy-Menge. Zu beachten ist, daß Menschen nur zur
Differenzierung von höchstens sieben bis elf Zugehörigkeitsgraden
im Stande sind.
Es sieht vielleicht problematisch oder sogar paradox aus, daß Repräsentation von Unschärfe
durch Mitgliedsgrade geschieht, die ihrerseits wieder genaue Zahlen sind. Obwohl dies bei den
meisten Anwendungen keine Probleme macht, kann man trotzdem das Prinzip der Fuzzy-Mengen verallgemeinern,
um den Unterschied zwischen verschiedenen Mitgliedsgraden zu verwischen. Mengen dieser Art werden
als Typ-2-Fuzzy-Mengen bezeichnet. Per Definition sind Typ-1-Fuzzy-Mengen normale Fuzzy-Mengen,
während Typ-2-Fuzzy-Mengen Typ-1-Fuzzy-Mengen als Elemente auf einer Universalmenge besitzen.
Auf diese Art können
höhere Typen definiert werden.
Alle Typ-2-Fuzzy-Mengen sind übrigens L-Fuzzy-Mengen.
Eine andere Art der Verallgemeinerung erhält man, wenn man Fuzzy-Mengen definiert, deren Elemente wiederum Fuzzy-Mengen sind. Diese Fuzzy-Mengen werden als Level-k-Fuzzy-Mengen bezeichnet, wobei k die Verschachtelungstiefe angibt. Beispiel für eine Level-2-Fuzzy-Menge wären ist die Sammlung von Attributen für ein neues Auto, wobei die Elemente der betrachteten Universalmenge normale (Level-1-) Fuzzy-Mengen wie billig, zuverlässig oder sportlich sind.
Die grundlegenden Verknüpfungen der klassischen Mengenlehre (Durchschnitt ![]() ,
Vereinigung
,
Vereinigung ![]() , Komplement ¯¯) sollen nun auch in geeigneter Weise für
Fuzzy-Mengen A und B eingeführt werden.
Von Zadeh wurden für die Modellierung der Operatoren ¯¯,
, Komplement ¯¯) sollen nun auch in geeigneter Weise für
Fuzzy-Mengen A und B eingeführt werden.
Von Zadeh wurden für die Modellierung der Operatoren ¯¯, ![]() und
und
![]() folgende Funktionen vorgeschlagen:
folgende Funktionen vorgeschlagen:
Wenn das Ergebnis der Mitgliedsfunktion von A und B auf die scharfe Menge ![]() beschränkt wird,
entsprechen diese Operatoren genau denen bei scharfen Mengen. Damit stellen diese Operatoren
eine Verallgemeinerung des üblichen Komplements, Durchschnitts und Vereinigung dar.
Diese Operatoren sind jedoch nicht die einzig denkbaren. Für jeden der drei Operatoren
wurden verschiedene Operatoren vorgeschlagen. Diese Operatoren müssen gewissen
Axiomen genügen, damit die Operatoren sinnvoll sind.
beschränkt wird,
entsprechen diese Operatoren genau denen bei scharfen Mengen. Damit stellen diese Operatoren
eine Verallgemeinerung des üblichen Komplements, Durchschnitts und Vereinigung dar.
Diese Operatoren sind jedoch nicht die einzig denkbaren. Für jeden der drei Operatoren
wurden verschiedene Operatoren vorgeschlagen. Diese Operatoren müssen gewissen
Axiomen genügen, damit die Operatoren sinnvoll sind.
Das Komplement einer Fuzzy-Menge A ist allgemein definiert durch eine Funktion
![]()
welche jedem Zugehörigkeitswert ![]() einen Wert
einen Wert ![]() zuordnet.
Dieser Wert wird interpretiert als der Zugehörigkeitsgrad von dem Element x in der
Fuzzy-Menge, welche die Negation des Konzeptes der Fuzzy-Menge A repräsentiert.
Wenn also z.B. A die Fuzzy-Menge aller großen Männer ist, ist das Komplement
die Fuzzy-Menge aller Männer, die nicht groß sind.
Offensichtlich gibt es viele Elemente, die sowohl einen positiven Zugehörigkeitsgrad
sowohl in sowohl ihrer Fuzzy-Menge, als auch in ihrem Komplement haben. Zum Vergleich:
dies ist in der klassischen Mengenlehre nicht möglich: entweder ist
zuordnet.
Dieser Wert wird interpretiert als der Zugehörigkeitsgrad von dem Element x in der
Fuzzy-Menge, welche die Negation des Konzeptes der Fuzzy-Menge A repräsentiert.
Wenn also z.B. A die Fuzzy-Menge aller großen Männer ist, ist das Komplement
die Fuzzy-Menge aller Männer, die nicht groß sind.
Offensichtlich gibt es viele Elemente, die sowohl einen positiven Zugehörigkeitsgrad
sowohl in sowohl ihrer Fuzzy-Menge, als auch in ihrem Komplement haben. Zum Vergleich:
dies ist in der klassischen Mengenlehre nicht möglich: entweder ist ![]() , oder
, oder
![]() , eine andere Möglichkeit gibt es nicht.
, eine andere Möglichkeit gibt es nicht.
Eine Funktion, die als Fuzzy-Komplement dienen soll, muß die Eigenschaften haben, sich am Rand bei 0 und 1 so verhalten wie das klassische Komplement, also c(0)=1 und c(1)=0. Desweiteren sollte die Funktion monoton fallend sein, da sonst ein größerer Eingabewert zu einem größeren Komplement führen würde, was der Vorstellung eines Komplementes widerspricht. Weiterhin ist oft wünschenswert (wenn auch nicht immer notwendig), daß die Funktion kontinuierlich definiert ist (keine Sprünge hat), sowie daß das Komplement des Komplements wieder der Ausgangswert ist (die Funktion muß involutorisch sein). Lediglich die in Gleichung 1 angegebene Funktion erfüllt alle diese Forderungen.
Ein Beispiel für das Komplement einer Fuzzy-Menge ist in Abbildung 13 gegeben.
Ein wichtiges Charakteristikum für das Komplement ist, wo eine Fuzzy-Menge F seinem
Komplement ![]() entspricht: wo ist
entspricht: wo ist ![]() . Bei der Standarddefiniton
ist dies bei
. Bei der Standarddefiniton
ist dies bei ![]() der Fall.
der Fall.
Man sieht also, daß sich scheinbare Widersprüche wie ``ist das Glas halb voll oder halb leer?'' sich in der Fuzzy-Theorie in Wohlgefallen auflösen: beide sind (wie auch intuitiv klar ist) identisch!
Sowohl der Schnitt als auch die Vereinigung zweier Mengen kann für Fuzzy-Mengen verallgemeinert werden. Die entsprechenden Operatoren bilden zwei Fuzzy-Mengen auf eine Fuzzy-Menge ab:
![]()
Für die Modellierung des Durchschnittes wird üblicherweise die Minimumsfunktion verwendet. Abbildung 14 verdeutlicht den Schnitt zweier Fuzzy-Mengen mittels der Minimumsfunktion.
Jede Funktion, die als Schnittmengenoperator dienen soll, muß verschiedene Eigenschaften haben: sie muß monoton, kommutativ und assoziativ sein, und außerdem muß der Schnitt einer (Fuzzy-)Menge mit der Gesamtmenge wieder die Ausgangsmenge ergeben. In der Mathematik wird eine Funktion, die diesen Bedingungen genügt, t-Norm (triangular, Dreiecks-Norm) genannt.
Die Vereinigung zweier Mengen wird analog zur Fuzzy-Schnittmenge eingeführt. Statt der Minimumfunktion wird hier jedoch üblicherweise die Maximumsfunktion verwendet. Abbildung 15 verdeutlicht die Vereinigung zweier Mengen mittels der Maximumsfunktion.
Verallgemeinert kann jede Funktion als Fuzzy-Vereinigungsoperator verwendet werden, die den Bedingungen einer t-Norm entspricht, jedoch muß die Vereinigung einer (Fuzzy-)Menge mit der leeren Menge wieder die Ausgangsmenge ergeben. Mathematisch spricht man hier von einer t-Conorm. Leicht zu sehen ist, daß jede t-Norm in eine entsprechende t-Conorm überführt werden kann: t-Conorm(a,b) = 1 - t-Norm(a,b).
Fuzzy-Mengen können mit Hilfe von verschiedenen Modifikatoroperationen verändert werden, um zum Beispiel Begriffe wie sehr, ziemlich und etwas zu modellieren. Üblich sind hier der Konzentrationsoperator, der für eine ``schärfer'' werden läßt, der Dilationsoperator, der eine Fuzzy-Menge ``unschärfer'' werden läßt, der Kontrastintensivierungsoperator, oder der Verschiebungsoperator, der eine Fuzzy-Menge nach ``links'' oder ``rechts'' verschiebt. Abbildung 16 verdeutlicht die Wirkungsweise verschiedener Fuzzy-Modifikatoren.
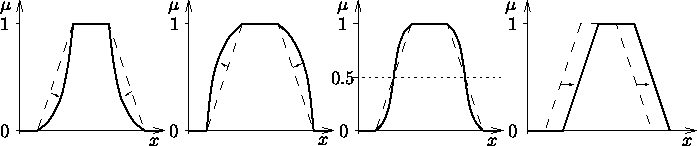
Abbildung 16: Wirkungsweise des Konzentrations-, Dilations-, Kontrastintensivierungs- und Verschiebungsoperators
Eine Relation R ist allgemein eine Teilmenge aus dem Kreuzprodukt ![]() mehrerer Grundmengen
mehrerer Grundmengen ![]() , formal
, formal
![]()
Der Begriff der Relation läßt sich auf Fuzzy-Relationen verallgemeinern.
Dabei geht man auch hier von einer Universalmenge U auf das Kreuzprodukt mehrerer
(nicht notwendigerweise verschiedener) Universalmengen ![]() über.
Eine n-stellige Fuzzy-Relation
über.
Eine n-stellige Fuzzy-Relation ![]() ist dann eine Abbildung
ist dann eine Abbildung
![]()
die jedem Tupel ![]() wieder einen
Zugehörigkeitswert im Intervall [0,1] zuordnet.
wieder einen
Zugehörigkeitswert im Intervall [0,1] zuordnet.
Ein Beispiel (nach [Zimmermann 1993, Seite 14]):
![]() =
= ![]() sei eine Menge von Personen {Anton, Bernd, Cäsar, Dagobert} und
sei eine Menge von Personen {Anton, Bernd, Cäsar, Dagobert} und ![]() die
unscharfe Relation ``größer als''. Dabei ist Anton 1,90m groß, Bernd 1,75m, Cäsar 1,65m
und Dagobert 1,85m. Die Fuzzy-Relation könnte folgendermaßen definiert sein:
die
unscharfe Relation ``größer als''. Dabei ist Anton 1,90m groß, Bernd 1,75m, Cäsar 1,65m
und Dagobert 1,85m. Die Fuzzy-Relation könnte folgendermaßen definiert sein:
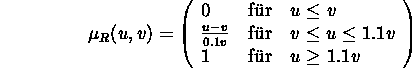
Die Zugehörigkeitsfunktion einer diskreten Fuzzy-Relation ``u größer als v'' kann in Matrixform wie folgt dargestellt werden:
u\v | Anton | Bernd | Cäsar | Dagobert |
| Anton | 0 | 0.857 | 1 | 0.27 |
| Bernd | 0 | 0 | 0.606 | 0 |
| Cäsar | 0 | 0 | 0 | 0 |
| Dagobert | 0 | 0.571 | 1 | 0 |
Interessant an Fuzzy-Relationen ist, daß diese gut benutzt werden können, um WENN...DANN... Regeln zu beschreiben (vgl. Abschnitt 3.4).
Linguistische Variablen sind eine spezielle Form von unscharfen Mengen. Die Werte bzw. Ausprägungen sind im Gegensatz zu numerischen Variablen nicht Zahlen, sondern Wörter oder Ausdrücke. Sie dienen dazu, sprachlich ausgedrücktes Wissen mit all seinen Unschärfen angemessen so zu modellieren, daß dabei möglichst wenig des Reichtums der menschlichen Sprache verloren geht, auf der anderen Seite jedoch das Wissen mit dem Computer verarbeitet werden kann. Mit dem Konzept der linguistischen Variablen ist es dann möglich, komplexe Systeme zu beschreiben, die mittels genauer mathematischer Modelle nicht in den Griff zu bekommen sind. Die in unserer Sprache enthaltene Unschärfe läßt sich gut durch linguistische Variable modellieren, deren einzelne Ausprägungen durch Fuzzy-Mengen repräsentiert werden. Beispiel: die linguistische Variable ``Badewassertemperatur'' läßt sich gut durch die fünf verbalen Terme ``kalt'', ``kühl'', ``angenehm'', ``warm'' und ``heiß'' charakterisieren. Eine stärkere Differenzierung ist oft möglich und sinnvoll. Üblich sind fünf bis zehn linguistische Terme pro linguistischer Variable (vgl. Abbildung 17).