Die meisten industriellen Anwendungen wurden im Bereich der Fuzzy-Regelung (auf diese wird weiter unten noch intensiv eingegangen) und der Fuzzy-Expertensysteme entwickelt. Andere industrielle Anwendungsgebiete für Fuzzy-Systeme sind z.B. [Kruse 1995, Seite 68]:
Die größten Erfolge im Bereich industrieller und kommerzieller Anwendungen von Fuzzy-Systemen wurden bisher durch Fuzzy-Regler (engl.: Fuzzy Controller) erzielt [Kruse 1995].
Wichtig ist der umgangssprachlich oft nicht beachtete Unterschied zwischen einer Regelung und einer Steuerung. Allgemein bedeutet Steuerung Größen durch andere, davon unabhängige, Größen zu beeinflussen. Steuervorgänge werden vor allem dort angewendet, wo auftretende Störgrößen einen konstanten, bekannten, oder nur geringen Einfluß auf die Regelgröße haben. Der Nachteil einer Steuerung liegt darin, daß das effektive Ergebnis der Steuerung nicht überwacht wird und damit keine Kontrolle stattfindet.
Genau dieses unterscheidet die Regelung von der Steuerung: bei der Regelung wird der Istwert einer Ausgangsgröße ständig gemessen und mit einer Führungsgröße (dem Sollwert) verglichen. Eine Differenz bewirkt eine angemessene Änderung der Eingangsgröße derart, daß der Differenz entgegengewirkt wird. Die Ausgangsgröße beeinflußt also die Eingangsgröße.
Das Prinzip der Steuerung und Regelung ist graphisch dargestellt in den Abbildungen 18 und 19.
Wie bei einem konventionellen Regler transformiert ein Fuzzy-Regler Eingangsgrößen (Sensormessungen)
in Ausgangsgrößen, die auf den Prozeß bzw. die Regelstrecke wirken.
Von außen betrachtet weist der Regler dabei keine ``Unschärfe'' auf. Die für Fuzzy-Systeme typische
Unschärfe wird im Innenbereich des Reglers benutzt.
Bei der Erstellung eines Fuzzy-Regelungssystemes wird folgendermaßen vorgegangen (vgl. [Kahlert 1994, S. 169 und 175]):
Jeder Fuzzy-Regler besteht aus drei verschiedenen Komponenten (vgl. Abbildung 20):
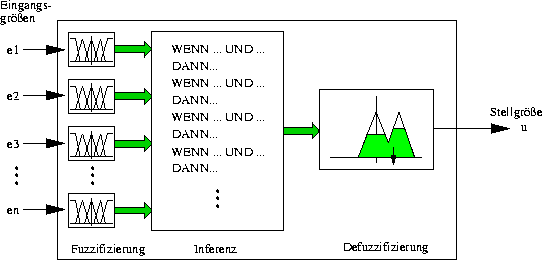
Abbildung 20: Logische Struktur eines Fuzzy-Reglers mit mehreren Eingangsgrößen und einer Ausgangsgröße
Die Eingangssignale werden dabei erst einmal ``fuzzifiziert'', es wird also zu jedem Eingangssignal der entsprechende Zugehörigkeitswert, also die entsprechenden Fuzzy-Mengen festgestellt. Diese Fuzzy-Mengen dienen dann als Eingabe für die Inferenzeinheit. In der Inferenzeinheit werden die einprogrammierten Regeln verwendet, um für jede Fuzzy-Menge zu bestimmen, in welchem Ausmaß sie zutrifft. Die Ergebnisse der verschiedenen Regeln werden dann in geeigneter Weise kombiniert, um aus den Ergebnissen der Inferenz ein scharfen Ausgangswert zu erzeugen. Dieser Schritt wird ``Defuzzifizierung'' genannt. Die einzelnen Schritte werden weiter unten noch ausführlicher erklärt.
Als Beispiel soll ein Fuzzy-Regler konstruiert werden, der abhängig von der Badewassertemperatur den Zufluß neuen Wassers so regeln soll, daß das Badewasser immer eine möglichst angenehme Temperatur hat (Fortführung des Beispieles aus 2.4). Dazu stehen zwei Wasserleitungen (``rot'' und ``blau'') zur Verfügung, die in ihrer Zuflußstärke gesteuert werden können (vgl. Abbildung 21).
Die Meßgröße (Eingangsgröße) ist die Temperatur eines in der Badewanne befestigten Meßfühlers. Die Öffnung der Ventile (zwischen offen und geschlossen) des roten und blauen Wasserstroms ist die zu regelnde Ausgangsgröße. Die linguistische Variable ``Badewassertemperatur'' wird mit dem Satz linguistischer Terme ``kalt'', ``kühl'' ``angenehm'', ``warm'', ``heiß'' modelliert. (vgl. Abbildung 17). Die linguistische Variable ``Temperaturzufuhr_blau'' (analog rot) wird mit dem Satz linguistischer Terme ``stark'', ``mittel'' und ``aus'' modelliert . (Abbildung 22).
Die Fuzzifizierung führt die den scharfen Meßwert der Temperatur in einen Vektor von Zugehörigkeitsgraden der linguistischen Variablen ``Badewassertemperatur'' über. Wenn wir einen Meßwert von 56 Grad annehmen (Abbildung 23), so ist die Fuzzy-Menge ``warm'' 0.31 erfüllt, und ``heiß'' 0.675. Das Wasser ist mit 56 Grad also zwischen warm und heiß, und zwar eher heiß. Der scharfe Wert 56 Grad wird zu einem Vektor (0.0, 0.0, 0.0, 0.31, 0.675) der Fuzzy-Variablen ``Badewassertemperatur'' (kalt, kühl, angenehm, warm, heiß).
Um die Temperatur des neu zugeführten Wassers abhängig von der aktuellen Temperatur zu machen, sind Regeln nötig, wie z.B.:
Nun wollen wir testen, in welchem Grad die Regeln betroffen sind. Wir gehen dazu alle Regeln der Reihe nach durch. Wir stellen fest, daß alle Regeln bearbeitet werden müssen.
Die Bedingung in Regel 1 ist nur zu 0.675 erfüllt, dementsprechend wird das Ergebnis Temperaturzufuhr_blau entsprechend gekürzt: wir schneiden die Fuzzy-Menge ``heiß'' der linguistischen Variablen Temperaturzufuhr_blau der Höhe 0.675 ab. Wir verfahren analog mit Regel 2. Das Ergebnis ist in Abbildung 24 zu sehen. Die Ergebnisse müssen jetzt noch kombiniert werden, hier nehmen wir jeweils das Maximum und erhalten die Fuzzy-Menge in Abbildung 25. Für die Temperaturzufuhr_rot erhalten wir die Fuzzy-Menge ``aus'' in der Höhe 0.675, dem Maximum von 0.675 und 0.31.
Die Fuzzy-Menge aus Abbildung 24 muß nun noch in einen scharfen Wert umgewandelt werden. Wie oben schon erwähnt, wird üblicherweise der Schwerpunkt der Fläche bestimmt, dieser dann auf die x-Achse projeziert, und der sich ergebende Wert wird dann als Ausgangswert benutzt. Für die Ausgangsvariable ``roter Ventil'' ergibt sich ``aus'' (der Schwerpunkt ist direkt über ``geschlossen''), für das ``blaue Ventil'' nach Abbildung 25 ein Öffnungsgrad des Ventils von ungefähr 86%.
Die Vorteile von Fuzzy-Reglern sind, daß diese eine recht schnelle,
realistische, problembezogene, aussagekräftigere Modellierung auch komplexer
Systeme mit nichtlinearem Verhalten ermöglichen. Dabei ist die Beschreibung
und das Verhalten eines Systems mit
linguistischen Ausdrücken möglich, was wesentlich einfacher ist als durch
mathematische Beschreibungsverfahren.
Ebenfalls angenehm ist die gute Wartbarkeit: falls die Regelung in einem
Bereich nicht gut ist, werden entsprechende Regeln ergänzt oder verändert,
bzw. die Definition der Fuzzy-Mengen verändert. Als positiv erweist sich
häufig die gute Nachvollziehbarkeit der Ergebnisse: die Regeln können der
Reihe nach notfalls auch per Hand durchgerechnet werden.
Die Nachteile von Fuzzy-Reglern, gerade gegenüber neuronalen Netzen, ist, daß diese nicht lernfähig sind. Damit ist keine automatische Anpassung an eine sich verändernde Umgebung möglich. Auch können Fehler in der Erstellungsphase später kaum wieder verbessert werden. Unangenehm bei den Defuzzifizierungsmethoden ist, daß es schwierig sein kann, die richtige Methode zu finden. Der Vorteil der Unschärfe wird durch Rückübersetzung in diskreten Wert oft zerstört. Die Berechnung des scharfen Endwertes ist entweder komplex, langsam und gut, oder schnell, dafür aber mit einem schlechteren Ergebnis. Hier gibt es also einen Trade-off zwischen Geschwindigkeit und Ergebnisgüte.
Bei dem Entwurf von Fuzzy-Reglern sind insbesondere die Aufstellung der Regelbasis, sowie die geeignete Modellierung der Fuzzy-Mengen problematisch. Durch die Kombination von Fuzzy-Reglern mit neuronalen Netzen können diese Nachteile recht gut kompensiert werden.
Bei adaptiven Fuzzy-Systemen existieren beide Teile selbstständig: das neuronale Netz und der Fuzzy-Regler. Der Fuzzy-Regler liefert dem neuronalen Netz Beispieldaten zur Verfügung, auf deren Basis das neuronale Netz eine optimierte Regelbasis erstellt, die dann dem Fuzzy-System für die Ausführung des Inferenzmechanismus zurückgegeben wird. Dadurch verlieren die Inferenzregeln ihren starren Charakter, das Fuzzy-System kann sich einer verändernden Umwelt (z.B. Verschleißerscheinungen) anpassen.
Hier verschmelzen das neuronale Netz und der Fuzzy-Regler zu einem
Gesamtsystem. Die Systeme existieren hier nicht mehr selbständig nebeneinander,
sondern gehen ineinander über: das Neuronale Netz übernimmt zusätzlich
zur Regelbasisoptimierung auch den Inferenzprozeß. Diese Systeme haben
den Vorteil, daß die Ein- bzw. Ausgangsdaten in fuzzy-typischer Form wie z.B.
sprachliche Ausdrücke vorliegen können, während die Optimierung durch die
Anpassungsfähigkeit und die Inferenz von einer neuronalen Struktur
vorgenommen wird.
Der zusätzliche Vorteil der adaptiven Fuzzy-Systemen ist, daß diese sich auch in sicherheitskritischen Bereichen einsetzten lassen, da die Regeln sich sowohl kontrollieren, als auch deren maximalen Ausprägungen vorschreiben lassen.
Fuzzy-Regler lassen sich nur relativ aufwendig durch Software implementieren. Die im Prinzip mögliche Parallelisierung wird dabei nicht ausgenutzt, und die Simulation analoger Werte zwischen 0 und 1 durch Gleitkommazahlen ist aufwendig und zeitintensiv. Dies hat schon relativ früh dazu geführt, daß Fuzzy-Regler direkt in Hardware implementiert wurden. Dies führt zu einer schnelleren Verarbeitungszeit, sowie einer starken Miniaturisierung. Ein Problem der meisten Fuzzy-Hardware-Regler ist die Effizienz der Defuzzifizierung. Die Schwerpunktmethode eignet sich hierfür kaum, da hier keine parallele Abarbeitung möglich ist und die dazu nötigen mathematischen Operationen recht aufwendig sind.
Fuzzy-Logic eignet sich wegen der guten Verarbeitung von vagen Informationen, wie sie in der Praxis recht häufig vorkommen (Medizin: hohes Fieber, etc.), gut für den Einsatz in Expertensystemen. Der wesentlichste Unterschied zu konventionellen Expertensystemen ist, daß Fuzzy-Expertensysteme keine Entscheidungsbäume durchlaufen, sondern wie bei der Fuzzy-Regelung Regeln partiell aktivieren und sie zu einem Gesamtergebnis verschmelzen. Damit kann auch widersprüchliches Wissen mehrerer Experten genutzt werden, was sonst nicht möglich ist: in konventionellen Systemen müssen die Regeln konsistent sein. Bei Fuzzy-Expertensystemen kann die Anzahl der Regeln, die normalerweise notwendig ist, um ein Wissensgebiet zu beschreiben, deutlich reduziert werden. Es wird von einer Reduktion der nötigen Regeln um den Faktor 100 bis 1000 gesprochen [McNeill 1996, Seite 309]. Damit kann die Entwicklungszeit eines Fuzzy-Expertensystems im Vergleich zu einem herkömmlichen Expertensystem oft wesentlich verkürzt werden. Andere Vorteile sind, daß für die Ermittlung einer Antwort nicht alle Informationen benötigt werden: vorhandene Daten werden ausgewertet und die zutreffensten Ergebnisse zurückgeliefert. Der strukturelle Aufbau eines Fuzzy-Expertensystems ist in Abbildung 26 wiedergegeben.